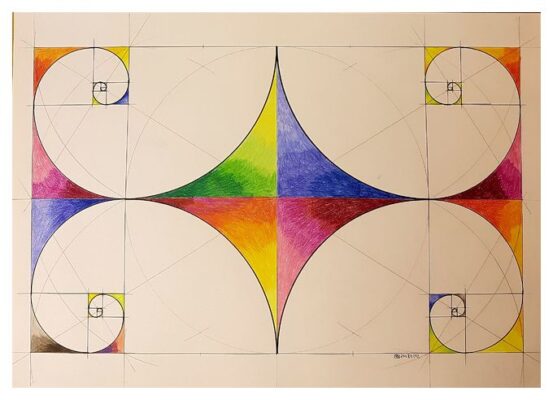
Ниже приведена последовательность Фибоначчи: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, Когда мы берем любые два последовательных (одно за другим) числа в последовательности, их соотношение очень близко к золотой пропорции. На самом деле, чем позже числа в последовательности, тем ближе она становится к золотой пропорции.
Как использовать золотое сечение в живописи? Шаг 1 — Постройте простой квадрат. Шаг 2 — Проведите линию по центру квадрата. Шаг 3 — Возьмите компас, поставьте одну точку на пересечении с серединой и проведите линию вниз от края правого верхнего угла, как показано ниже. Шаг 4 — Завершите золотой прямоугольник.
Как последовательность Фибоначчи используется в искусстве?
Художники признали, что спираль Фибоначчи является выражением эстетически приятного принципа — правила третей. Это правило используется в композиции картины; уравновешивая элементы изображения по третям, а не строго центрируя их, достигается более приятное течение картины.
Золотое сечение и Фибоначчи — это одно и то же?
Золотое сечение описывает предсказуемые закономерности во всем — от атомов до огромных звезд на небе. Это соотношение происходит от последовательности Фибоначчи, названной в честь ее итальянского основателя Леонардо Фибоначчи. Природа использует это соотношение для поддержания баланса, и финансовые рынки, похоже, тоже.
Как построить золотое сечение?
Золотое сечение можно найти, если разделить линию на две части, и большая часть (a), деленная на меньшую часть (b), равна сумме (a) + (b), деленной на (a), которая равна 1,618. Эта формула может помочь вам при создании фигур, логотипов, макетов и многого другого.
Почему была создана последовательность Фибоначчи?
Последовательность Фибоначчи была получена в результате математической задачи о разведении кроликов, которая была поставлена в Liber Abaci.
Почему последовательность Фибоначчи так важна?
Последовательность Фибоначчи значима из-за так называемого золотого сечения 1,618, или обратного ему 0,618. В последовательности Фибоначчи любое число приблизительно в 1,618 раз больше предыдущего, если не учитывать первые несколько чисел.